Параметры КЭ и интенсивность напряжений в металлоконструкциях подъёмных машин

Изусова Л.В., Московская Государственная Академия Водного Транспорта

Оценка влияния параметров конечных элементов (КЭ) сети на величину коэффициента интенсивности напряжений (КИН) в программном комплексе Autodesk Simulation Mechanical.

Одним из наиболее часто встречающихся дефектов металлоконструкций подъёмных и перегрузочных машин, в том числе, портовых и плавучих кранов, являются усталостные трещины.

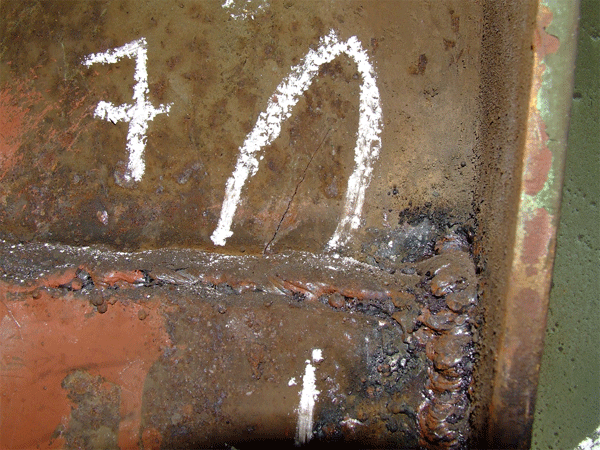
Рис. 1. Трещина, расположенная в труднодоступном месте металлоконструкции крана, небольшой протяжённости.

Согласно действующим на данный момент требованиям Ростехнадзора обнаруженные трещины подлежат немедленному устранению. Требования Российского Речного Регистра (РРР) в этом случае оказываются более гибкими: трещины должны быть устранены, но допускается (на усмотрение комиссии, проводившей обследование) устранять трещины при текущем или капитальном ремонте, проводимом после окончания навигации. При этом эксперты РРР, как правило, требуют устранять трещины согласно технологии, разработанной специализированной организацией и согласованной в органах РРР. Как показывает опыт, ремонт трещин, выполненный в спокойной обстановке, квалифицированными сварщиками с соблюдением технологических требований позволяет избежать появления трещин в отремонтированных узлах при их дальнейшей эксплуатации.

Особняком стоит вопрос о не распространяющихся трещинах, которые также встречаются в металлоконструкциях. Как уже говорилось, устранение трещин в металлоконструкциях грузоподъёмных машин является обязательным требованием всех надзорных органов. В то же время устранение некоторых не распространяющихся трещин может привести к ухудшению состояния узла конструкции.

В процессе технического диагностирования грузоподъёмных кранов возникают ситуации, когда необходимо принять решение о возможности эксплуатации металлоконструкции с трещиной в течение некоторого времени. Основой для принятия такого решения должна служить оценка напряжённого состояния как узла в целом, так и в вершине трещины. Провести такую оценку позволяет использование метода конечных элементов (МКЭ) и программных продуктов на его основе. В качестве базового программного комплекса для исследования напряжённого состояния на нашей кафедре был выбран Autodesk Simulation Mechanical (ASM), хорошо известный специалистам в области КЭ моделирования под прежним названием Algor.

На первом этапе исследования встал вопрос: что использовать в качестве параметра для оценки НДС в вершине трещины коэффициент интенсивности напряжений (КИН) или J-интеграл? После анализа имеющейся литературы выбор был сделан в пользу КИН, поскольку величины пороговых Kth, критических Kfc КИН и вязкости разрушения Kc, основанные на экспериментальных данных достаточно полно представлены в отечественных изданиях, чего нельзя сказать о значениях J-интеграла. Определение величины КИН в программе ASM производится прямым методом по полю перемещений в окрестности вершины трещины.

Рис. 2. Разбиение на конечные элементы (а - регулярное, б - нерегулярное).

Следующим этапом в решении поставленной задачи стала верификация результатов расчёта. Для этого были рассмотрены несколько задач, для которых имеются аналитические решения. В качестве тестовых использовались задачи о пластине конечной ширины с центральной и краевой трещинами. Решения для указанных задач были получены в плоской и пространственной постановке с варьированием ряда параметров разбиения и оценки значения КИН. В качестве варьируемых параметров разбиения были приняты следующие:
- характер КЭ сети - регулярная или нерегулярная (см. рис. 1);
- радиус сгущения КЭ сети в окрестности трещины (R);
- размер КЭ в зоне сгущения сетки (r);
- количество рядов КЭ в окрестности вершины трещины, учитываемых при определении КИН (n).

В качестве верификационных критериев были приняты относительные ошибки для среднего (Δmean, %) и максимального (Δmax, %) значений КИН, полученных МКЭ в сравнении с теоретическим расчётом.
В результате было установлено следующее:
Решение задачи МКЭ в плоской постановке (с использованием 2D-элементов) всегда даёт завышенное (относительно теоретического) значение КИН на величину около 200%.
Решения, полученные с использованием регулярной КЭ сети, при прочих равных условиях, позволяют получить более близкие к теоретическим результаты (Δmax = -2...5%, Δmean = -5...-2%), по сравнению с нерегулярной сеткой (Δmax = 3...36%, Δmean = -19...1%). Причём точность расчёт при использовании регулярной сетки незначительно зависит от размера КЭ r и количества рядов n.
При расчётах с нерегулярной КЭ сеткой наиболее адекватные результаты получены в тех случаях, когда выполняются соотношения: r/a ≤ 0,1; R/a ≥ 2; R/r ≥ 20 и n = 2...4, где a - характерный размер трещины (длина краевой трещины принята равной a, центральной - 2а). В этом случае относительные ошибки по максимальным значениям КИН составляют Δmax = 4...12%, а по средним значениям КИН - Δmean = -2...2%.
Таким образом, для адекватной оценки значения КИН МКЭ с использованием программы ASM может быть рекомендовано разбиение моделей с использованием регулярной КЭ сетки, а там, где это невозможно - с использованием рекомендуемых параметров разбиения.
Кроме того, перспективным для дальнейших исследований представляется оценка КИН не прямым методом, а через значения J-интеграла.

Иллюстрации:

Рис. 3. Фрагмент опорного барабана крана КПЛ 5-30 с результатами расчёта.

Рис. 4. Сравнение результатов расчёта КИН МКЭ при моделировании средней трещины в пластине конечной ширины с результатом расчёта по аналитической формуле. Результат неудовлетворительный.

Рис. 5. Регулярная сетка. Выполнено сгущение сетки в окрестности вершин трещин. Все конечные элементы 8-ми узловые типа brick.

Рис. 6. Сравнение результатов расчёта КИН МКЭ при моделировании средней трещины в пластине конечной ширины с результатом.

Рис. 7. Распределение КИН по фронту трещины при регулярной разбивке.

Рис. 8. Нерегулярная КЭ сетка в окрестности вершины трещины. Трещина смоделирована острым надрезом. Элемент моделировался объёмными элементами типов brick (8-ми узловой) и tetrahedra (6-ти узловой).

Рис. 9. Сравнение результатов расчёта КИН МКЭ при моделировании средней трещины в пластине конечной ширины с результатом расчёта по аналитической формуле. Элемент моделировался объёмными элементами типов brick (8-ми узловой) и tetrahedra (6-ти узловой). Разбивка нерегулярная, сетка сгущается в окрестности вершины трещины, ограниченной радиусом 5...10 мм. Погрешность расчёта не превышает от -50 до -2%. Результат неудовлетворительный.

Рис. 10. Распределение КИН по фронту трещины при нерегулярной разбивке. Видна явная неравномерность этого распределения, что является ещё одним подтверждением неудовлетворительности расчёта.

Рис. 11. Окончательный вариант подготовки детали под расчёт КИН. Максимальный размер ячейки в окрестности вершины трещины r = 0,05 мм, размер области сгущения сетки вокруг вершины трещины определяется по формуле R=4∙r. Сама трещина моделируется разрезом шириной 2∙r, до области сгущения сетки. В области сгущения зазор между берегами трещины задаётся равным нулю, при этом на берегах создаются контактные элементы типа Free/No contact.

Рис. 12. Разбивка на КЭ окончательного варианта.

Рис. 13. Сравнение результатов расчёта КИН МКЭ при моделировании средней трещины в пластине конечной ширины с результатом расчёта по аналитической формуле. Элемент моделировался объёмными элементами типа brick (8-ми узловой) и tetrahedra (6-ти узловой). Результат удовлетворительный.

Рис. 14. Распределение КИН по фронту трещины в окончательном варианте расчёта.